Sharpe Ratio
夏普率
定義
- 由 William Sharpe (經濟諾貝爾獎得主) 提出。
- 用來衡量投資組合的風險調整後的回報。
- 衡量「在承受 1% 的風險下,能得到多少報酬?」
- 例如:夏普率 0.5,代表承受 1% 的波動風險下,長期可以創造 0.5% 的報酬率。
- 也可以說:想得到 5% 的報酬,可以預期過程有 10% 的上下波動。
- 例如:夏普率 0.5,代表承受 1% 的波動風險下,長期可以創造 0.5% 的報酬率。
- 常被用在基金成效、資產配置等長期投資的成效衡量。
- 例如:有兩種金融商品,風險都是一樣的,夏普值越高,代表報酬也越高,也有點像是 CP 值的概念,把成本換成風險。
計算公式
-
- 預期報酬率:投組或個股回報率。
- 無風險利率:如:美國公債、銀行定存。
- 標準差:過去一段時間價格上下變動起伏,標準差越大,波動性越大。
如何計算
- 報酬率、標準差應使用「每日」的報酬數值計算。
- 公式 (詳細):
-
- 252 平方根:因一年約 252 交易日,用以將波動數值從每日調整成年。
-
- EXCEL 公式:
- Average():取平均值
- Stdev():取標準差
- SQRT():取平方根 (或
{ #0}
.5)
- 數據不能取太短,最好包含多頭、空頭。
- 例如:計算至少要包含到 2008 年才有參考價值 (因近年多為多頭市場)。
- 好的策略,取任何一段時間的夏普率,數值不應有巨大落差。
- 可使用分段測試 (Rolling test) 檢視。
夏普率高低的差異
- 夏普值越高,代表報酬越高 (在相同風險下),類似 CP 值的概念。
- 例如:S&P500 vs 股債平衡:
- S&P500:波動大 (2008 年 -50%),Sharpe Ratio 0.53。
- 股債平衡:相對平穩 (2008 年 -20%),Sharpe Ratio 0.94。
- 如何衡量好壞?
- 0.5 上下:單純買進持有指數 (如 S&P500) 的水準。
- 接近 1:不錯的策略 (通常經過資產配置)。
- 1.5 以上:非常優秀。
效率前緣 (Efficient Frontier)
- 效率前緣:顯示某風險水平下的最高回報投資組合。
- Sharpe Ratio 可用來判斷投資組合是否位於效率前緣。
- 最大化 Sharpe Ratio 的投資組合稱為「市場投資組合」,被認為是最佳風險回報點。
Sharpe Ratio 的限制
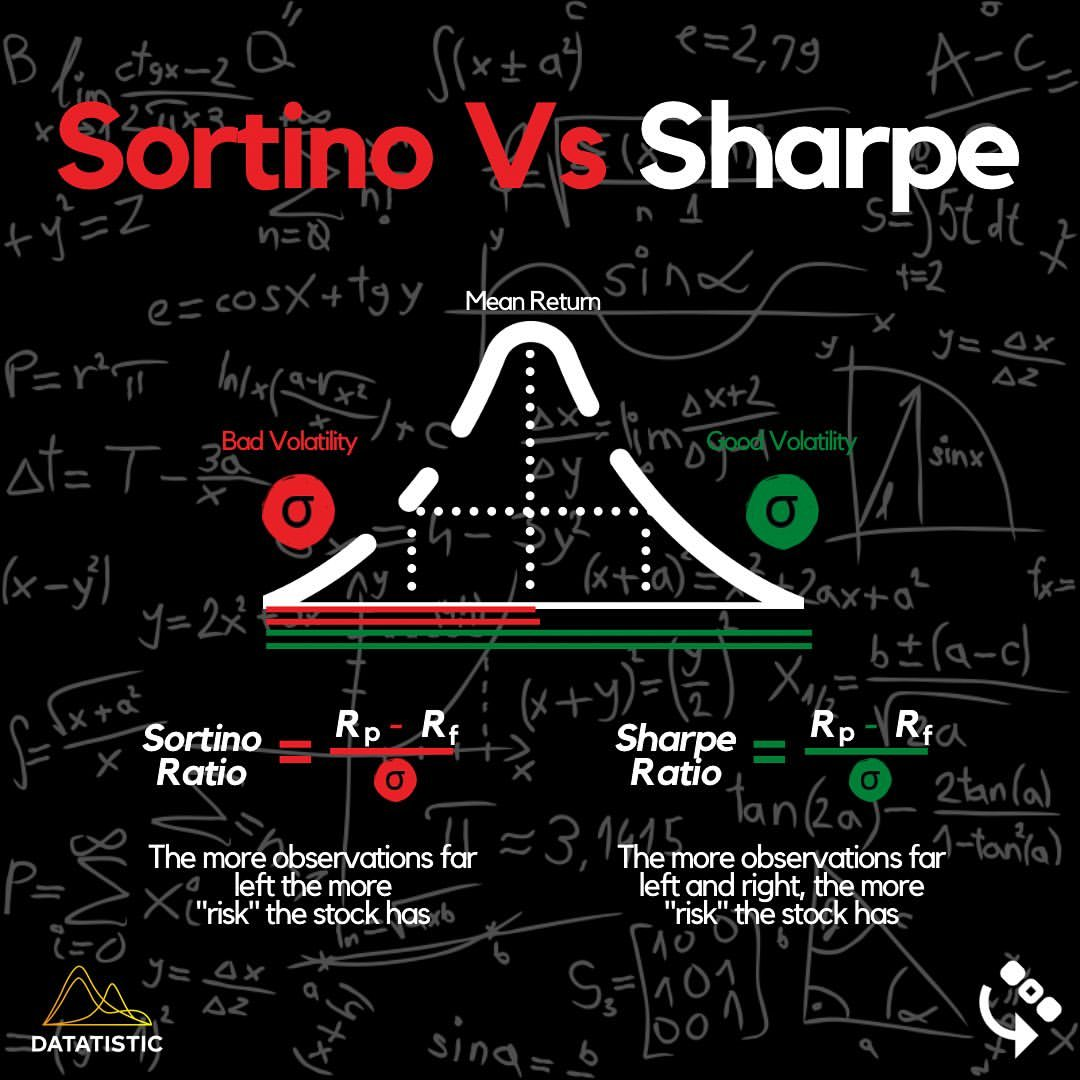
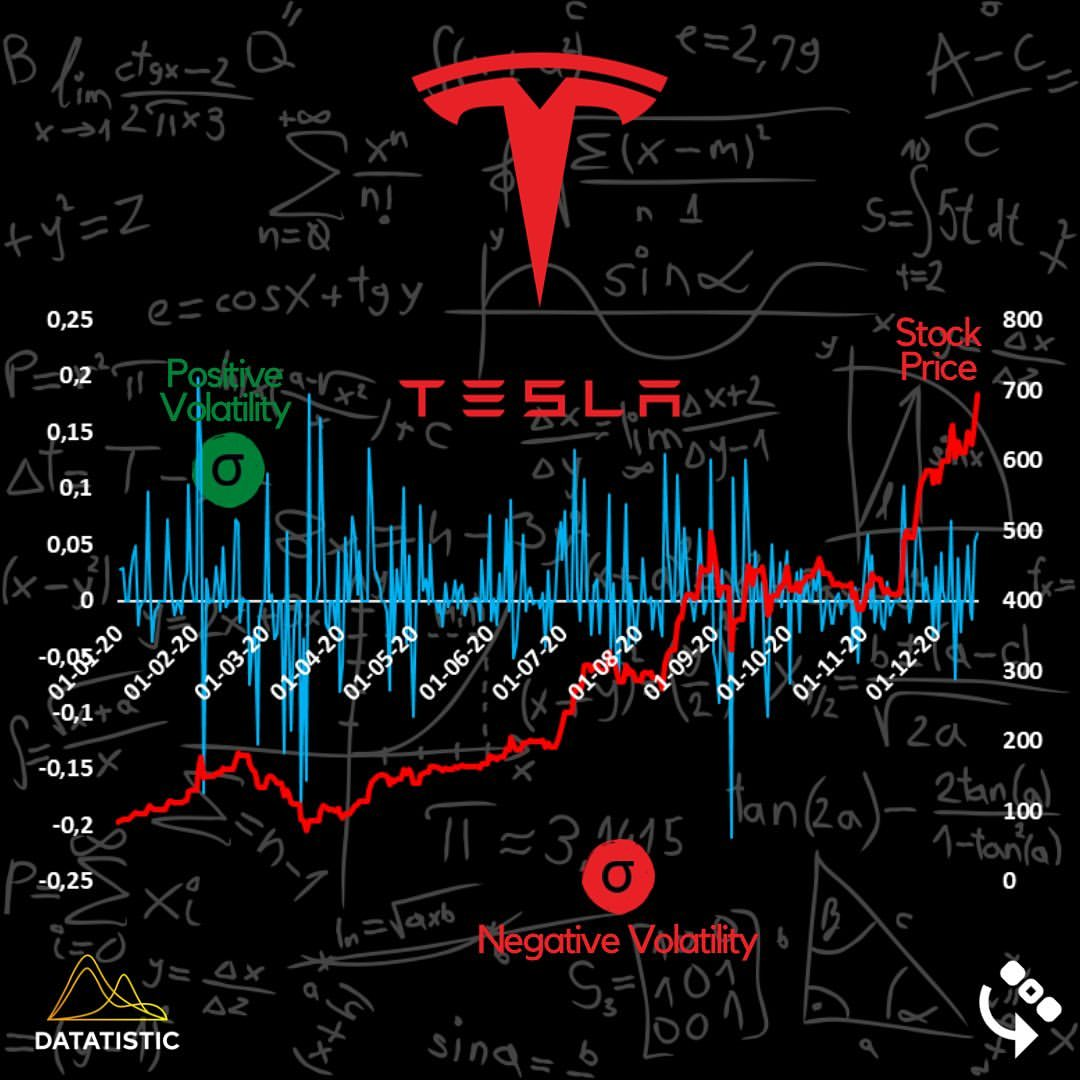
- 忽視正負波動差異:所有波動都視為風險,未分好壞。
- 在非常態分佈中效果差:若回報分佈有偏態或峰態,解釋力下降。
解決方案:Sortino Ratio
- 更注重下行風險:只關注負面波動。
- 適合穩健型投資者:能更真實反映穩健策略的風險。
比較
- Sharpe Ratio:適合衡量總體回報/風險,與效率前緣理論相關。
- Sortino Ratio:適合專注下行風險的情境。
- 兩者結合使用能更全面地評估投資策略的風險與回報。